Representación de funciones complejas usando el método de dominio coloreado
Las siguientes imágenes fueron creadas con GeoGebra. Applets interactivos se pueden encontrar en el siguiente enlace:
Las versiones en línea son un poco lentas, por lo que recomiendo descargarlos a tu computadora. Para ello usa el enlace:
El método usado para crear todas las imágenes se explica en el siguiente artículo:
Esquema HSL:
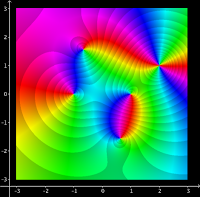
Esquema HSV con retrato de fase, curvas de nivel del módulo y fase de la función $(z-1)/(z^2+z+1)$:
Esquema HSV para visualizar ramas y puntos de corte de funciones multivaluadas:
Esquema HSV con curvas de nivel de las componentes real e imaginara y el módulo $|f(z)|$:
Miscelánea de funciones:
Referencias
Las versiones en línea son un poco lentas, por lo que recomiendo descargarlos a tu computadora. Para ello usa el enlace:
El método usado para crear todas las imágenes se explica en el siguiente artículo:
Esquema HSL:
Esquema HSV con retrato de fase, curvas de nivel del módulo y fase de la función $(z-1)/(z^2+z+1)$:
|
Retrato de fase simple
|
Retrato de fase con curvas de nivel del módulo $|f|$
|
|
Retrato de fase con curvas de nivel de $\text{Arg}(f(z))$
|
Retrato de fase combinado
|
Esquema HSV para visualizar ramas y puntos de corte de funciones multivaluadas:
$z^{1/2}$
$\log z$
$\arctan z$
Esquema HSV para la clasificación de singularidades:
|
$(1-\cosh z)/z^3$
Singularidad orden 1
|
$\exp(2z)/(z-1)^2$
Singularidad orden 2
|
$\sinh z/z^4$
Singularidad orden 3
|
Esquema HSV con curvas de nivel de las componentes real e imaginara y el módulo $|f(z)|$:
Miscelánea de funciones:
|
$\frac{(1/z)^{18}-(1/z)}{1/z-1}$
|
$\sum_{n=1}^{20}\frac{z^n}{1-z^n}$
|
$\sin(1/z^2)$
|
|
$\sqrt{1-1/z^2+z^3}$
|
$\dfrac{\left(z-2-i\right)^2\left(z^2-1\right)}{z^2+2+i}$
|
$z^{2/3+i}$
|
|
$\sqrt{1-z^2}$
|
$\frac{z+i}{z-1}$
|
$\exp(1-z^2)-1$
|
Referencias
- Ablowitz, M. J. & Fokas, A. S. (2003). Complex variables: introduction and applications (2nd ed). Cambridge University Press.
- Breda, A. Trocado, A. & Santos, J. (2013). O GeoGebra para além da segunda dimensão. Indagatio Didactica, 5(1). Recuperado el 12 de junio de 2018, de http://revistas.ua.pt/index.php/ID/article/view/2421
- Crone, L. (s.f) Color graphs of complex functions. http://fs2.american.edu/lcrone/www/ComplexPlot.html
- Farris, F. (1997). Visualizing complex-valued functions in the plane. Recuperado el 12 de junio de 2018, de http://www.maa.org/pubs/amm_complements/complex.html
- Farris, F. A. (1998). Review of Visual Complex Analysis. By Tristan Needham. American Mathematical Monthly 105 (1998), 570–576.
- Losada Liste, R. (2014). El color dinámico de GeoGebra. Gaceta De La Real Sociedad Matemática Española, 17, 525–547, Madrid. Recuperado el 12 de junio de 2018, de http://www.geogebra.es/color_dinamico/Color%20dinamico%20-%20GacRSocMatEsp.pdf
- Lundmark, H. (2004). Visualizing complex analytic functions using domain coloring. Recuperado el 12 de junio de 2018, de http://users.mai.liu.se/hanlu09/complex/domain_coloring.html
- Needham, T. (1997). Visual Complex Analysis. Oxford University Press, Oxford.
- Marsden, J. E. & Hoffman, M. J. (1987) Basic Complex Analysis. (2nd ed.) W. H. Freeman and Co, New York.
- Wegert, E. (2010). Phase diagrams of meromorphic functions. Comput. Methods Funct. Theory 10, 639-661.
- Wegert, E. (2012). Visual Complex Functions: An introduction with phase portraits. New York: Springer Basel.
- Wegert, E. & Semmler, G. (2011). Phase plots of complex functions: a journey in illustration. Notices Amer. Math. Soc. 58, 768-780.
- Wikipedia: Domain Coloring Recuperado el 12 de junio de 2018, de https://en.wikipedia.org/wiki/Domain_coloring




































Comentarios
Publicar un comentario