Proyección estereográfica (en dimensión 2)

Lo expuesto en esta entrada se relaciona y amplía lo expuesto aquí

Considere el plano $\mathbb{R}^2$, la esfera unitaria $S^2$ y $N=(0,0,1)$ su polo norte. Pruebe que $\mathbb{R},\:S^2\backslash{N}$ son espacios homeomorfos.

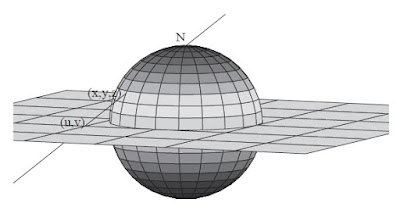
Solución. Definiremos una función $f:S^2\backslash\{N\}\to \mathbb{R}^2$ como sigue: dado el punto $(x,y,z)\in S^2\backslash{N}$ consideramos la línea que une a $N$ con $(x,y,z)$; el punto de intersección de dicha línea con el plano $\mathbb{R}^2\subset \mathbb{R}^3$ es el valor de $f(x)$. Observemos que la función $f$ manda el hemisferio inferior de la esfera al disco unitario en $\mathbb{R}^2$ y el hemisferio superior al exterior del disco. Véase la figura de abajo. 

También puedes usar el siguiente applet: Mueve el punto A definido en la esfera. Puedes cambiar la perspectiva 3d con el ratón.

Enlace: https://ggbm.at/bQKwnfN8

Para conocer las coordenadas de la función $f$ hagamos $f(x,y,z)=(u,v)$ y denotamos $r^2=x^2+y^2,\;s^2=u^2+v^2$. Observemos que se tienen dos triángulos semejantes como se muestra en la figura: 

Por la semejanza se tiene que

$$\frac{r}{1-z}=\frac{s}{1}\Leftrightarrow \frac{s}{r}=\frac{1}{1-z}.$$  

Proyectando dichos triángulos a los planos $y=0, x=0$ se obtiene

$$\dfrac{x}{1-z}=u,\qquad \dfrac{y}{1-z}=v.$$

De aquí tenemos que $f(x,y,z)=(u,v)=\frac{1}{1-z}(x,y)$ donde se observa que $f$ es continua. Obtendremos el resultado buscado mostrando que $f$ es homeomorfismo dando explícitamente a su inversa para lo cual usamos las relaciones anteriores:

$$\begin{eqnarray}\label{eq1}  \frac{x}{1-z}=u,\qquad \frac{y}{1-z}=v,\qquad \frac{r}{1-z}=s,\qquad z^2=1-r^2 \end{eqnarray}$$

De la relación ($\ref{eq1}$) se obtiene que $$1+s^2=\frac{(1-z)^2+r^2}{(1-z)^2};$$  

y como $z^2=1-r^2$ obtenemos $$1-z=\frac{2}{1+s^2}.$$ Dado que $x=u(1-z),y=v(1-z)$ se tiene que 

$$x=\dfrac{2u}{1+s^2},\qquad y=\dfrac{2v}{1+s^2}$$

y finalmente $$z=\frac{s^2-1}{1+s^2}.$$

Con lo que definimos $f^{-1}:\mathbb{R}^2\to S^2\backslash \{N\}$ mediante

$$f^{-1}(u,v)=(x,y,z)=\dfrac{1}{1+s^2}(2u,2v,s^2-1).$$

Claramente $f^{-1}$ es una función continua por lo que $f$ es homeomorfismo y el resultado se obtiene.

Nota final. El argumento anterior (y una de las figuras) fue tomado del libro Topology: a geometric approach de T. Lawson. Invitamos al lector a consultar el libro para cerciorarse que la elección del polo norte $N$ es totalmente arbitraria: es posible escoger otro punto y obtener espacios homeomorfos.