Acerca de Los Elementos de Euclides: algunos ejemplos en geometría dinámica

Los comienzos [de la Matemática] tuvieron una base intuitiva y empírica. El rigor se convirtió en una necesidad con los griegos, y -aunque se lograra poco hasta el siglo XIX- por un momento pareció alcanzado. Pero todos los esfuerzos por perseguir el rigor hasta el final han conducido a un callejón  sin salida, donde ya no hay acuerdo sobre qué significa realmente. La matemática sigue viva y con buena salud, pero solo mientras  se apoye en una base pragmática.

Morris Kline (1992, p. 1599)

1. Un poco de historia de Euclides

Euclides (330 a.C. - 275 a.C.) fue un matemático griego. En realidad se conoce muy poco su vida, pese a ser uno de los matemáticos más famosos de la Antigüedad.

Posiblemente Euclides estudió en Atenas, lo cual explica su conocimiento de la geometría elaborada en la escuela de Platón, aunque no parece que estuviera familiarizado con las obras de Aristóteles. Enseñó en la ciudad de Alejandría, donde alcanzó gran fama y prestigio durante el reinado de Tolomeo I Sóter.

Euclides fue autor de diversos tratados, sin embargo su nombre se asocia principalmente a Los Elementos, que rivaliza por su difusión con las obras más famosas de la literatura universal, como la Biblia o el Quijote. En esencia, Los Elementos son una compilación de obras de autores anteriores a Euclides (entre los que destaca Hipócrates de Quíos). Los Elementos se han transmitido a lo largo de 24 siglos a través de miles de ediciones y en diversas lenguas como el Griego original, el Árabe, el Latín y lenguas modernas como Inglés, Alemán, Euskera, Castellano, Catalán, entre muchas otras.

2. Los Elementos

Los Elementos son en sí una compilación sustancial de conocimiento matemático. Fue utilizado durante más de dos mil años como libro de estudio de contenidos matemáticos. En Los Elementos se introdujo la noción de demostración y la ordenación lógica de los teoremas, y su contenido determinó el curso del pensamiento matemático posterior.  

En conjunto son 132 definiciones, 5 postulados, 5 nociones comunes o axiomas y unas 465 proposiciones distribuidas en 13 libros. Entre los comentadores árabes se extendió la creencia de que el tratado incluía otros dos libros, el XIV y el XV, que complementaban el estudio de los sólidos regulares del libro XIII.

La teoría de la geometría plana se encuentra contenida en los libros I-IV; la geometría del espacio en XI-XIII; la teoría generalizada de la proporción en V-VI; la teoría aritmética en VII-IX; el libro X da una conceptualización precisa de la inconmesurabilidad y una clasificación prolija de las variedades de rectas irracionales. La mayoría de los temas contenidos en Los Elementos se mantienen actuales en programas de estudio de matemáticas. De hecho, durante varios siglos, en diversas universidades alrededor del mundo, fue utilizado para la enseñanza de la geometría. Actualmente se utiliza como una introducción básica a la geometría.

Es importante resaltar que el contenido de Los Elementos está basado en construcciones elementales con regla y compás. Sin embargo, lo que ha llamado más la atención es el conjunto de definiciones, postulados y nociones comunes, con la que inicia el Libro.

3. Algunos contenidos de Los Elementos

3.1 El pórtico axiomático

El libro I empieza con definiciones, algunas de ellas son:

1. Un punto es lo que no tiene partes

2. Una línea es longitud sin anchura

3. Los extremos de una línea son puntos

4. Una línea recta es aquella que yace por igual respecto de los puntos que están en ella.

5. Una superficie es lo que solo tiene longitud y anchura

15. Un círculo es una figura plana comprendida por una línea tal que todas las rectas que caen sobre ella desde un punto interior son iguales entre sí.

16. Y el punto se llama centro del círculo.

23. Son rectas paralelas las que estando en el mismo plano y siendo prolongadas indefinidamente en ambos sentidos no se encuentran una  a otra en ninguno de los dos sentidos.

Después Euclides postula lo siguiente:

1. (Es posible) trazar una línea de cualquier punto a cualquier punto;
2. (Es posible) prolongar una recta finita continuamente en línea recta;
3. (Es posible) describir un circulo con cualquier centro y distancia;
4. Que todos los ángulos rectos son iguales ente sí;
5. Que si una línea recta al caer sobre dos rectas hace los ángulos interiores de un mismo lado menores que dos ángulos rectos, entonces las dos rectas si son prolongadas indefinidamente se encontraran por el lado en el que están los ángulos menores que dos rectos. 

El soporte de los elementos se remata con una selección de nociones comunes:

            (1) cosas iguales a una misma cosa son también iguales entre sí

(2) si cosas iguales se añaden a cosas iguales, los totales son iguales

(3) si cosas iguales se sustraen de cosas iguales, los restos son iguales

(4) las cosas que coinciden entre sí, son iguales

(5) el todo es mayor que la parte

3.2 Algunas proposiciones

Como ya he mencionado, Los Elementos contienen alrededor de 465 proposiciones. A continuación presento algunos ejemplos del Libro I, II y III.


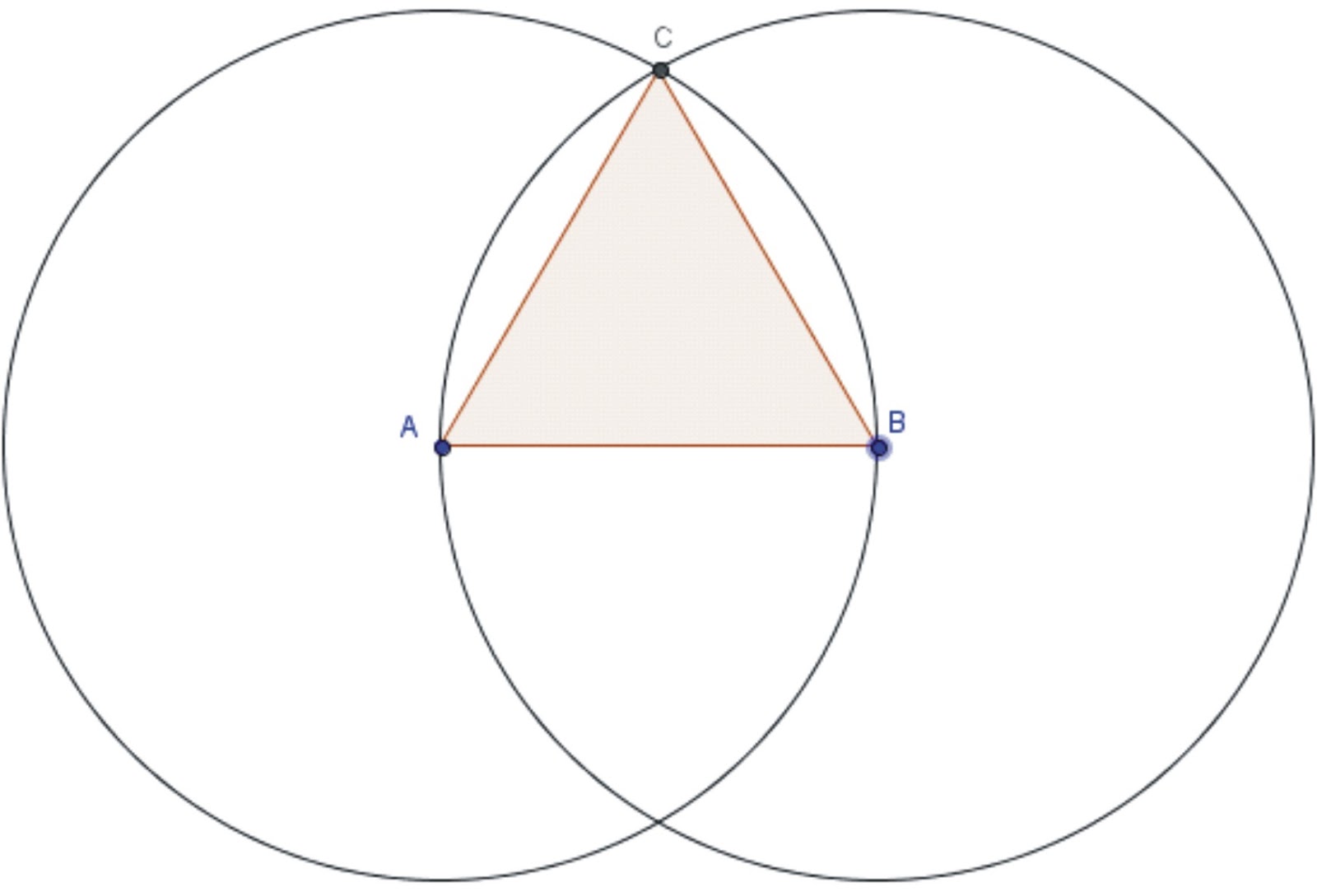
Proposición 1 (Libro I). Construir un triángulo equilátero sobre una recta finita dada.

Proposición 11 (Libro I). Trazar una línea recta que forme ángulos rectos con una recta dada, desde un punto dado en ella.

Proposición 47 (Libro I). En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto.

Nota: Esta proposición se refiere al Teorema de Pitágoras. Ver Applet html hecho en GeoGebra.

Proposición 4 (Libro II). Si se corta al azar una línea recta, el cuadrado de la (recta) entera es igual a los cuadrados de los segmentos y dos veces el rectángulo comprendido por los segmentos.

Proposición 5 (Libro II). Si se corta una línea recta en (segmentos) iguales y desiguales, el rectángulo comprendido por los segmentos desiguales de la (recta) entera junto con el cuadrado de la (recta que está) entre los puntos de sección, es igual al cuadrado de la mitad.

Proposición 11 (Libro II). Dividir una recta dada de manera que el rectángulo comprendido por la (recta) entera y uno de los segmentos sea igual al cuadrado del segmento restante.

Nota: Ver Applet html de Geogebra aquí.

Proposición 21 (Libro III). En un círculo los ángulos en el mismo segmento son iguales entre sí.

Proposición 22 (Libro II). Los ángulos opuestos de los cuadriláteros en los círculos son iguales a dos rectos.

 

4. Comentarios Finales

La forma de presentación de las proposiciones no es originalmente de Euclides, pero sí es suya la forma de presentación del conjunto de la obra: La exposición de los axiomas al inicio, la explícita declaración de cada una de las definiciones y el ordenado encadenamiento de los teoremas, dispuestos de forma que vayan de los más simple a lo más complejo.

Aunque los matemáticos generalmente consideraron a Euclides como un modelo de rigor hasta bien entrado el siglo XIX, hay en el serios defectos que algunos matemáticos detectaron y de hecho combatieron. El primero es el empleo de la superposición. EI segundo, la vaguedad de algunas definiciones y las imprecisiones de otras. Por ejemplo, las definiciones iniciales de punto, línea y superficie no tienen sentido matemático preciso y, como ahora sabemos, no se les puede dar ninguno porque cualquier desarrollo matemático independiente debe incluir términos indefinidos. Incluso hay defectos en las demostraciones propuestas. Algunos son errores debidos a Euclides que pueden corregirse, aunque en ciertos casos se requeriría una nueva demostración. Otro tipo de defecto que recorre todos los Elementos es la afirmación de un teorema general del que sólo se prueba algún caso especial o para posiciones especiales de los datos propuestos  (Kline, 1992, pp. 126-127). 

A pesar de estos defectos, Los Elementos tuvieron tanto éxito que desplazaron a todos los textos de geometría anteriores. En el siglo III a. C., cuando aún se disponía de tratados de geometría, incluso Apolonio y Arquímedes se remitían a Los Elementos para citar resultados anteriores a ellos.

En la actualidad permanecen vigentes como material de referencia y de estudio de diversos contenidos matemáticos e incluso de estudio no sólo matemático sino también filosófico.

Referencias

• Euclides.  (1991). Los Elementos. Libros I-IV. Madrid: Gredos. (Col. Biblioteca Clásica Gredos #155). Traducción del griego al español de Ma. Luisa Puertas Castaños.
• Euclides.  (1994). Los Elementos. Libros V-IX. Madrid: Gredos. (Col. Biblioteca Clásica Gredos #191). Traducción del griego al español de Ma. Luisa Puertas Castaños.
• Euclides.  (1996). Los Elementos. Libros X-XIII. Madrid: Gredos.  (Col. Biblioteca Clásica Gredos #228). Traducción del griego al español de Ma. Luisa Puertas Castaños.
• Kline, M. (1992). El pensamiento matemático de la antigüedad a nuestros días. Alianza Editorial. Madrid, España.