Representación dinámica de transformaciones complejas

Una función compleja $f(z)$ se puede considerar como un mapeo o transformación de los puntos en el plano $z$ (con $z=x+iy$) a los puntos en el plano $w$ (donde $u+iv$).

El applet abajo muestra algunas transformaciones básicas de regiones simples (cuadrados). Por ejemplo:

$f(z)=1/z$ con  $-1/2\leq \text{Re}(z)\leq1/2,$ $-1/2\leq \text{Im}(z)\leq1/2$ y $z\neq 0$.

$f(z)=e^z$ con  $-\frac{\pi}{2}\leq \text{Re}(z)\leq\frac{\pi}{2},$ $-\frac{\pi}{2}\leq \text{Im}(z)\leq\frac{\pi}{2}$.

Las siguientes imágenes muestran transformaciones de funciones complejas cuando se consideran regiones rectangulares discretas de puntos. 

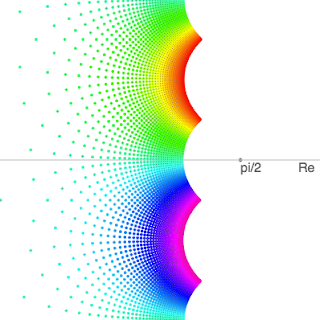
$f(z)=\log(z)$ with  $-\frac{\pi}{2}\leq \text{Re}(z)\leq\frac{\pi}{2},$ $-\frac{\pi}{2}\leq \text{Im}(z)\leq\frac{\pi}{2}$ y $z\neq 0$.

$f(z)=\text{sen}(z)$ with  $-\frac{\pi}{2}\leq \text{Re}(z)\leq\frac{\pi}{2},$ $-\frac{\pi}{2}\leq \text{Im}(z)\leq\frac{\pi}{2}$.

$f(z)=z+\frac1z$ with  $-0.6\leq \text{Re}(z)\leq0.6,$ $-0.6\leq \text{Im}(z)\leq0.6$ y $z\neq 0$.

$f(z)=z^2$ with $-1\leq \text{Re}(z)\leq1,$ $-1\leq \text{Im}(z)\leq1$.

$f(z)=z^{1/2}$ with $-1\leq \text{Re}(z)\leq1,$ $-1\leq \text{Im}(z)\leq1$ y $z\neq 0$.