Bestiario Topológico

Entradas

Mostrando las entradas de abril, 2017

Mostrar todo

Proyección estereográfica (en dimensión 2)

De Miguel A. Maldonado - abril 23, 2017

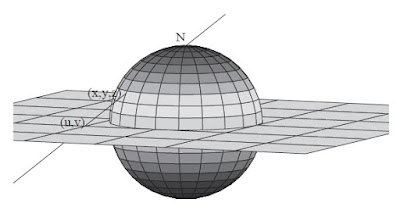
Lo expuesto en esta entrada se relaciona y amplía lo expuesto aquí Considere el plano

$\mathbb{R}^2$ , la esfera unitaria

$S^2$ y

$N=(0,0,1)$ su polo norte. Pruebe que

$\mathbb{R},\:S^2\backslash{N}$ son espacios homeomorfos. Solución. Definiremos una función

$f:S^2\backslash\{N\}\to \mathbb{R}^2$ como sigue: dado el punto

$(x,y,z)\in S^2\backslash{N}$ consideramos la línea que une a

$N$ con

$(x,y,z)$ ; el punto de intersección de dicha línea con el plano

$\mathbb{R}^2\subset \mathbb{R}^3$ es el valor de

$f(x)$ . Observemos que la función

$f$ manda el hemisferio inferior de la esfera al disco unitario en

$\mathbb{R}^2$ y el hemisferio superior al exterior del disco. Véase la figura de abajo. También puedes usar el siguiente applet: Mueve el punto A definido en la esfera. Puedes cambiar la perspectiva 3d con el ratón. Enlace: https://ggbm.at/bQKwnfN8 Para conocer las coordenadas de la función

$f$ hagamos

$f(x,y,z)=(u,v)$ y denotamos $r^2=x^2+y^2...

Ejercicio de Topología

De Miguel A. Maldonado - abril 23, 2017

Considere a los espacios

$\mathbb{R}^2, \mathbb{R}$ con métrica usual y defina la función

$p: \mathbb{R}^2\to \mathbb{R},\qquad p(x,y)=x$ Pruebe que

$p$ es función continua. Solución . Para

$(x,y)\in \mathbb{R}^2$ tomemos

$V$ vecindad de

$x\in \mathbb{R}$ y consideremos

$\epsilon$ tal que

$B_\epsilon(x)\subseteq V$ . Definamos

$U=B_\epsilon((x,y))$ y notemos que

$p(U)\subseteq V$ , lo cual prueba que

$p$ es continua.

Buscar este blog

Bestiario Topológico

Entradas

Proyección estereográfica (en dimensión 2)

Ejercicio de Topología

Entradas populares

Galileo Galilei y su ley de caída libre

Una historia de la Teoría de Conjuntos

Breve historia del Cálculo