Función Riemann integrable, discontinua en un conjunto denso
En 1854 el matemático alemán Georg Friedrich Bernhard Riemann (1826-1866) publicó su trabajo: Ueber die Darstellbarkeiteiner Function durch eine
trigonometrische Reihe (se puede consultar aquí, en la página 228). Riemann abordó el tema de integrabilidad para funciones más generales. Básicamente, él desarrolló una teoría de integración, con base en
las ideas de Augustin Louis Cauchy (1789-1857), debilitando las condiciones necesarias para que una
función sea integrable.
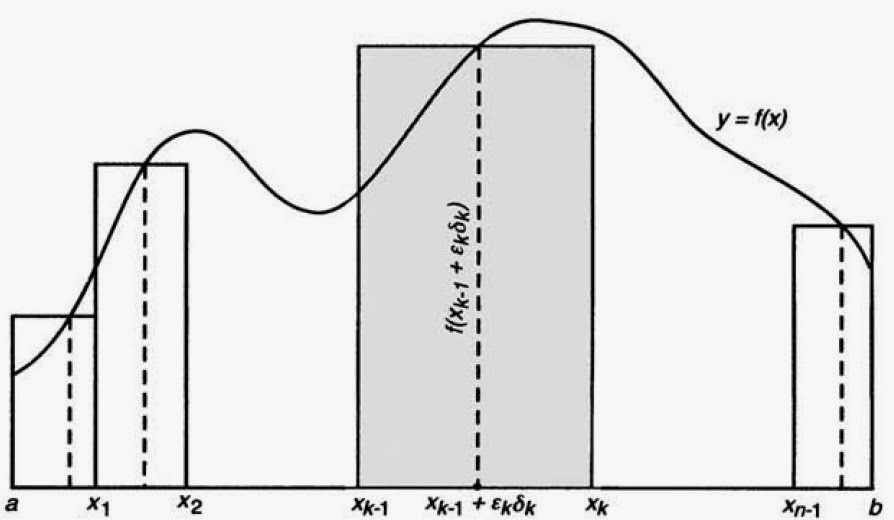
Suponiendo que $f(x)$ es una función acotada en el intervalo $[a,b]$, Riemann consideró una partición $a=x_0,x_1,\ldots , x_n=b$ del intervalo $[a,b]$. Él denotó las longitudes de los sub-intervalos resultantes como $\delta_k=x_k-x_{k-1}$ con $k=0,1,\ldots , n$. Después, Riemann consideró una sucesión $\epsilon_k$ de números reales tales que $0<\epsilon_k < 1$ para definir $t_k=x_{k-1}+\epsilon_k \delta_k$, que por consecuencia tenemos $t_k \in [x_{k-1},x_k]$ para cada $k=0,1,\ldots , n$. Entonces Riemann introdujo la suma
$$S_n=\sum_{k=1}^{n}f(t_k)(x_k-x_{k-1})$$
conocida actualmente como suma de Riemann. Esta suma es el total de las áreas de los rectángulos de cada sub-intervalo con base $\delta_k$ y altura $f(x_{k-1}+\epsilon_k \delta_k) $, como se muestra en la siguiente Figura:
Si la suma $S_n$, sin importar la elección de $\delta_k$ y $\epsilon_k$, tiene la propiedad de que se aproxima suficientemente a un valor fijo $A$ mientras que $\delta_k$ se vuelve suficientemente pequeño, entonces este valor fijo se denota por
$$\int_a^bf(x)dx.$$
Un ejemplo donde se puede apreciar el uso de sumas de Riemann, para funciones continuas, es el siguiente applet:
La definición anterior, establecida en términos de sumatorias más generales, se aplica a funciones acotadas no necesariamente continuas en un intervalo o también a funciones con discontinuidades aisladas, lo cual hace la diferencia respecto a la definición dada por Cauchy.
Condición 1:
$$\lim_{||P || \rightarrow 0} \sum_{k=1}^n D_k \delta_k=0$$
donde $\delta_k=x_k-x_{k-1}$, $P$ es una partición del intervalo $[a,b]$ y $D_k$ denota la oscilación de $f(x)$ en el correspondiente subintervalo.
Geométricamente, la anterior condición se puede apreciar en la siguiente Figura:
En seguida, Riemann demostró que la Condición 1 se puede remplazar por una condición equivalente.
Condición 2:
Para todo $\epsilon>0$ y $\delta>0$, existe $d>0$ tal que si $||P ||<\delta$, entonces $s(P,\delta )=$ {suma de las longitudes de los intervalos $I$, de la partición $P$ en los que la oscilación de $f$ es $\geq \delta$} es menor que $\epsilon$.
$$\int_a^bf(x)dx.$$
Un ejemplo donde se puede apreciar el uso de sumas de Riemann, para funciones continuas, es el siguiente applet:
La definición anterior, establecida en términos de sumatorias más generales, se aplica a funciones acotadas no necesariamente continuas en un intervalo o también a funciones con discontinuidades aisladas, lo cual hace la diferencia respecto a la definición dada por Cauchy.
Condición 1:
$$\lim_{||P || \rightarrow 0} \sum_{k=1}^n D_k \delta_k=0$$
donde $\delta_k=x_k-x_{k-1}$, $P$ es una partición del intervalo $[a,b]$ y $D_k$ denota la oscilación de $f(x)$ en el correspondiente subintervalo.
Geométricamente, la anterior condición se puede apreciar en la siguiente Figura:
En seguida, Riemann demostró que la Condición 1 se puede remplazar por una condición equivalente.
Condición 2:
Para todo $\epsilon>0$ y $\delta>0$, existe $d>0$ tal que si $||P ||<\delta$, entonces $s(P,\delta )=$ {suma de las longitudes de los intervalos $I$, de la partición $P$ en los que la oscilación de $f$ es $\geq \delta$} es menor que $\epsilon$.
El
mismo Riemann enfatizó el hecho de que su definición se aplica para funciones
más generales, en particular, incluye la posibilidad de integrar funciones con infinitos puntos de discontinuidad en cada intervalo. En el mismo trabajo, citado al inicio, Riemann presentó un ejemplo de una función discontinua en un conjunto
denso, la cual es integrable.
Ejemplo
de Riemann:
Sea
$$f(x)=\sum_{n=1}^{\infty}\frac{(nx)}{n^2}$$
donde $(x)=x-m(x)$ si $x\neq (2k+1)/2$ y $(x)=0$ si $x=(2k+1)/2$ (con $m(x)$ igual al entero más próximo a $x$).
Sea
$$f(x)=\sum_{n=1}^{\infty}\frac{(nx)}{n^2}$$
donde $(x)=x-m(x)$ si $x\neq (2k+1)/2$ y $(x)=0$ si $x=(2k+1)/2$ (con $m(x)$ igual al entero más próximo a $x$).
Es
posible realizar un esbozo de la función anterior. Para ello se debe considerar
la expresión
$$f(x)=\sum_{n=1}^{k}\frac{(nx)}{n^2}$$
para
$k$ un número entero suficientemente grande. La siguiente figura muestra
una animación para diferentes casos de $k$.
GeoGebra Applet: Aquí puedes ver la función en GeoGebra
Notemos que la función es discontinua en cada punto de la forma
$$x=\frac{m}{2n}$$
donde $m$ y $2n$ son primos relativos. En realidad, para estos valores $x$, el límite por la derecha y la izquierda de $f$ en $x$ son:
$$\lim_{z\rightarrow x^+}f\left( z\right) =f\left( x\right)-\frac{1}{2n^2}\sum_{i=0}^{\infty}\frac{1}{(2i+1)^2}=f\left( x\right) -\frac{\pi^2}{16n^2}$$
y
$$\lim_{z\rightarrow x^-}f\left( z\right) =f\left( x\right)+\frac{1}{2n^2}\sum_{i=0}^{\infty}\frac{1}{(2i+1)^2}=f\left( x\right) +\frac{\pi^2}{16n^2}$$
De esta manera, $f$ es discontinua en un subconjunto infinito denso de los números reales. Sin embargo, $f$ es integrable, pues en cada intervalo finito hay un número finito de puntos $x=\frac{m}{2n}$ en los que el salto
$$\left|\lim_{z\rightarrow x^+}f\left( z\right) - \lim_{z\rightarrow x^{-}}f\left( z\right) \right|=\frac{\pi^2}{8n^2}$$
sea mayor que un $\delta>0$ fijo y por tanto se cumple la condición 2, mencionada arriba.
Gracias por llegar al final de este artículo. Si deseas puedes apoyarme en Patreon usando el siguiente enlace:
Become a Patron!Con tu apoyo podré seguir escribiendo y compartiendo artículos y applets de matemáticas.





Comentarios
Publicar un comentario